Pythonでlog(x)のグラフを描いて理解する「(自己)情報量」

(自己)情報量の式って、logとか入っててなんか複雑だなぁ、と思う方は多いのではないでしょうか？
ここでは、(自己)情報量の式E = -log⁡ 𝑝(𝑥)を覚え、その性質を理解した後、-log𝑥のグラフをPythonで描いて見ることで(自己)情報量の理解を定着させます。
したがって、このコンテンツでは、数学だけでなくPythonプログラミングも一緒に勉強します。

本日のお品書きはこちら。

(自己)情報量とは何か？
(自己)情報量は区間の狭い単調減少関数
Pythonでlog(x)のグラフを描いてみるプログラム紹介
Google Collaboratoryでの実行例
まとめ

1. (自己)情報量とは何か？

(自己)情報量は、ある事象が起こることがどのくらい珍しいことかを数値化したものです。
𝑥が起こる確率を𝑝(𝑥)とすると、その珍しさをE = -log⁡ 𝑝(𝑥)で表します。

-log⁡(𝑝(𝑥))は、珍しい事象に対しては値が大きくなり、珍しくない事象に対しては値が小さくなるという、
珍しさを数値化するのに適した性質を持った式なのです。

2. (自己)情報量は区間の狭い単調減少関数

でも、なぜE = -log⁡(𝑝(𝑥))は、そのような「珍しさ」を表現するのに都合のよい性質を持っているのでしょうか？
それは、この関数に以下の性質があるからです。

(自己)情報量の区間は狭い(0≤𝑝(𝑥)≤1)
確率𝑝(𝑥)が、0～1の間の値にしかならないから
その区間(0≤𝑝(𝑥)≤1)内で、(自己)情報量は単調減少関数
𝑝(𝑥)=0では∞、そこからどんどん減っていき、𝑝(𝑥)=1のとき0になる

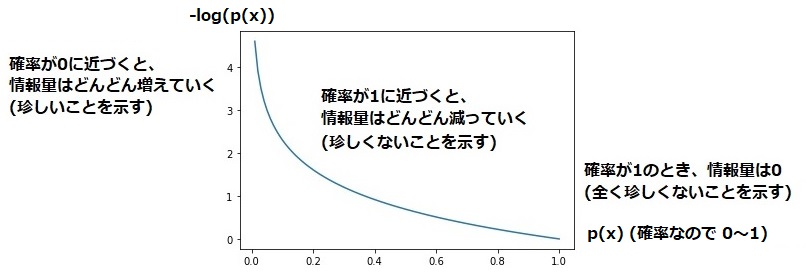
つまり、E = -log𝑝(𝑥)は、有効な区間となる0≤𝑝(𝑥)≤1の間、確率𝑝(𝑥)が小さいほど値が大きく、確率𝑝(𝑥)が大きいほど値が小さいという、「珍しさ」を表現するのにとても都合のよい性質を持っているのです。

以下の図で、その様子をグラフで確認しましょう。

3. Pythonでlog(x)のグラフを描いてみるプログラム

さて、このグラフをPythonで描くプログラムを身につけましょう。E資格向けには、数学とPythonを一度に勉強できて一石二鳥です。

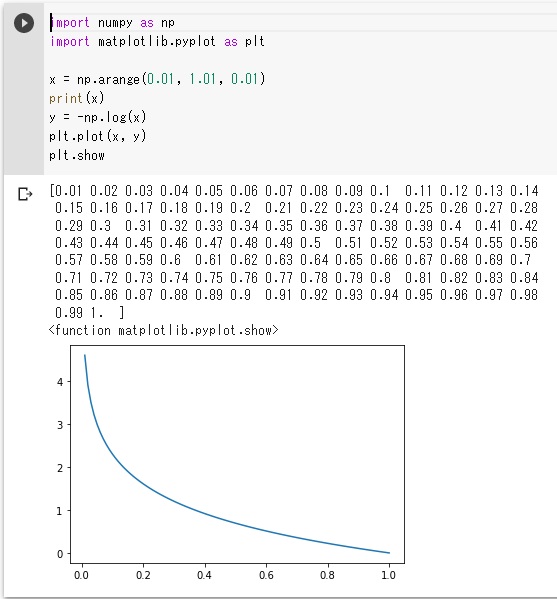
4. Google Collaboratoryでの実行例

指に覚えさせたら、ぜひPython環境で実行してみましょう。以下はGoogle Collaboratoryでの実行結果です。

5. 本日のまとめ

(自己)情報量は、ある事象が起こることがどのくらい珍しいことかを示します。
𝑥が起こる確率を𝑝(𝑥)とすると、その珍しさをE = -log⁡ 𝑝(𝑥)で表します。

E = -log⁡(𝑝(𝑥))は、珍しい事象に対しては値が大きくなり、珍しくない事象に対しては値が小さくなるという、
珍しさを数値化するのに適した性質を持った式でした。

(自己)情報量の式はlogを含んでいますので、「難しそう！」と思ってしまうかもしれません。
しかし実際は、「確率は0～1の間の値にしかならない」ことから、区間0≤𝑝(𝑥)≤1のときの-log𝑝(𝑥)の性質さえ知っておけば十分でした。
そして皆さんは、そのグラフを描くためのPythonプログラムを指に覚えさせましたので、今後何も心配することはありません。

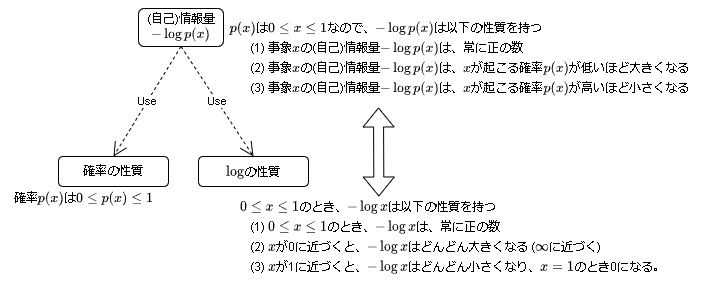
本日紹介した知識を１枚のシートにまとめてみました。ご参考まで。